Step two: Risk vs. return assessment methodology

In our previous article related to measuring nonprime returns and associated risks, we addressed the importance of having a consistent quantitative framework for measuring return and risk. Having a risk-return framework allows institutions to approach capital allocation more objectively than simply categorizing whole asset classes as “too-risky”. Moreover, even for institutions not expanding into new asset classes, explicitly defining this framework illuminates the historical accuracy of risk-return decisions within asset classes already in the institution’s comfort zone and may even help identify potential underwriting improvements.
Recognizing the need for objectively and quantifying risk does not immediately solve the problem. Other questions remain:
- How should risk be measured?
- How should risk be assessed relative to expected returns?
- How sophisticated an approach does an institution with limited resources actually need?
We will explore these questions below and discuss a proposed methodology.
From Risk-Free to Higher Yields
Within financial institutions the risk of suffering a financial loss is often categorized into either a credit risk or a market risk. With respect to credit and market risk, cash is the only asset that has neither. US Treasuries are also considered to have zero credit risk with progressively longer duration Treasuries subject to increasing market risk from yield curve fluctuations. As these Treasury instruments are still free of credit risk their yields are typically used to determine the risk-free interest rate over a given time horizon.
Investments that are not risk-free should be expected to earn more than the risk-free rate. The expected excess return of a given asset can thus be computed as follows:
Excess Return = E[Ra] – Rf
E[Ra] = expected return on asset A
Rf = risk-free yield
Using Market Risk Measurements for Credit Risk
For market risk, the expected volatility or standard deviation of an asset’s returns is typically used as a proxy for measuring the “riskiness” of an asset and the amount of loss that may be suffered within certain probabilistic bounds. Indeed, for market risk knowing only an asset’s expected return and expected return standard deviation already enables us to compute the well-known Sharpe Ratio to determine whether certain assets are providing more return relative to their amount of risk than other assets (assets with higher Shape Ratios offer a more attractive risk-return tradeoff):
Sharpe Ratio = (E[Ra] – Rf ) / σa
σa = return standard deviation of asset A
But can the Sharpe Ratio be applied to loans that are not actively traded? Yes, and it is not difficult – one must only estimate the probability of default and the expected loss given default – both figures that financial institutions extending credit should be experienced in determining. The other key inputs for applying the Sharpe Ratio to credit risk are the risk-free interest rate (which is set to 2.5% in the table below for illustrative purposes) and the yield of the loan. Indeed, the yield on the loan can be toggled higher or lower by the institution making the decision to extend credit so as to target a specific Sharpe Ratio hurdle.
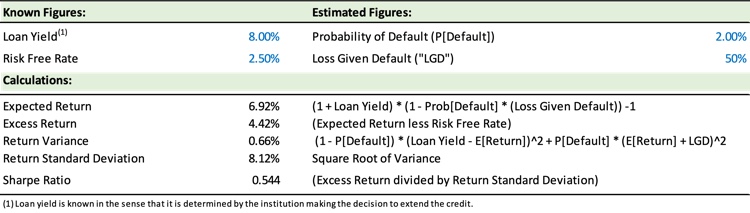
By applying the Sharpe Ratio to measuring credit risk-return opportunities financial institutions can provide themselves with a consistent quantitative methodology for assessing the stand-alone relative risk-return attractiveness of specific loan originations or loan participations for any asset class or lending opportunity. Using a Sharpe Ratio approach also means that the institution will have a common methodology for assessing both market risk and credit risk. Such a common methodology also positions the institution to potentially further leverage decades of market risk measurement practices should it wish to invest additional resources in doing so.
Having a quantitative framework in place to assess risk-return decisions also enables the institution to undertake additional risk management analyses. For example, an institution interested in computing with 95% confidence “Value at Risk” on the entirety of a loan pool with a large number of loans could simply take the expected return and then subtract two (2) standard deviations of return. Using the figures in the above table to represent a hypothetical pool of a large number of non-prime loans implies a projected maximum loss of ~9% with 95% confidence (i.e., 6.92% – (2 * 8.12%)).
Beyond the Sharpe Ratio
Using a risk-reward appraisal approach based on the Sharpe Ratio for evaluating lending and participation opportunities in both new and existing loan assets classes would be an excellent “second” step for institutions that currently do not have an explicit quantitative framework. The reason financial institutions can easily take this step with little additional investment is because (as credit underwriters) they are well-equipped to estimate a loan’s (i) probability of default and (ii) the expected loss given default.
Unfortunately, at present, it remains significantly more difficult for these same credit underwriters to reliably estimate the same loan’s return covariance with other loans, assets classes or broader indices, to establish the loan’s non-diversifiable co-volatility in the same manner that a stock’s Beta has been easily calculated for decades. This makes it more difficult to quantitively determine the positive impacts of increased diversification when entering new asset classes, geographies or credit strata. However, technology and improved market infrastructure continue to foster the development of liquid markets for assets, such as loans, that were previously relegated to permanent hold-to-maturity status. In time, this may allow institutions to use additional well-established market risk management measures to complement their existing credit risk management framework.
Co-authored by Michael Lanzarone





